Peamine erinevus: Parabool on kooniline osa, mis tekib siis, kui lennuk lõikab koonuse külje paralleelselt koonilise pinna. Hüperbool tekib siis, kui lennuk lõikab teljega paralleelselt koonilise pinna.

Parabool ja hüperbool on kaks erinevat sõna, sektsiooni ja võrrandit, mida kasutatakse matemaatikas, et kirjeldada kahte koonuse erinevat osa. Need on erineva kuju, suuruse ja mitmesuguste muude tegurite hulgas, et lisada valemid, mida kasutatakse selle arvutamiseks. Nende mõistmiseks mõistame kõigepealt koonust ja erinevaid koonuseid.

Koonusosa on kõver, mis saadakse, kui lennuk lõikub koonusega erinevalt. Ristmikul saadud lõiked hõlmavad ellipsi, ringi, parabooli ja hüperboola. Analüütilise geomeetria kohaselt on koonus defineeritud kui „taseme algebraline kõver 2. astme juures”. Koonuse sektsiooni populaarne määratlus sisaldab fookuspunkti, suunda ja ekstsentrilisust. Fookuspunkt ja otsesuunalised jooned on eeldatavasti koonuselises fikseeritud ratsioonis. Seda suhet nimetatakse koonuse osa ekstsentrilisuseks. Ellipsi, paraboolide ja hüperboolide ekstsentrilisus on erinev; ellipsi ekstsentrilisus on väiksem kui 1, paraboolide ekstsentrilisus on võrdne 1-ga ja hüperboolide ekstsentrilisus on suurem kui 1. Varaseim teadaolev töö kooniliste osade puhul võib pärineda neljandast sajandist eKr. lahendada kuubiku kahekordistamise probleem paraboolide abil.

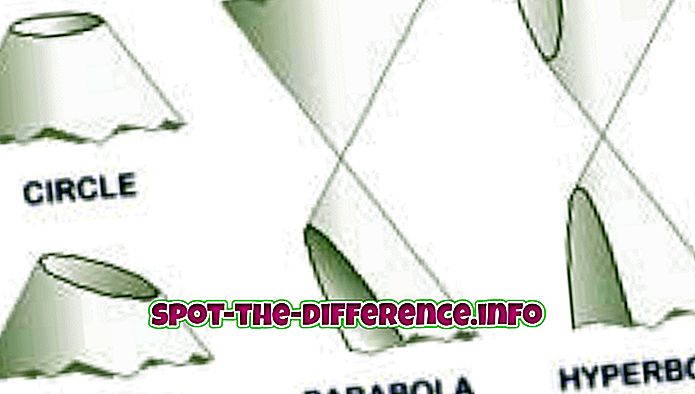
Parabool on koonusosa, mis tekib, kui lennuk lõikub koonusega. Parabolae või paraboolide vorm „parempoolse ümmarguse koonilise pinna ja selle pinna genereeriva sirgjoonega paralleelse tasapinna lõikumisest”. Teine viis, kuidas parabool luuakse, on see, kui fookusest ja otsesuunast ühtlaselt asetseva tasapinna punktid loovad parabooli. Algebras kasutatakse paraboole tavaliselt ruutude funktsioonides, kasutades valemit y = x ^ 2.

Rida, mis jagab parabooli keskel, on tuntud kui sümmeetriatelg; see rida on ka suunda suhtes risti ja läbib fookust. Punkte, mis paiknevad parabooliga ristuval sümmeetriateljel, nimetatakse "tipuks". Pikkuse ja fookuse vaheline kaugus on tuntud kui „fookuskaugus”. Parabolas saab avada mõlemas suunas, sealhulgas üles, alla, paremale või vasakule. Paraboolide peamiseks tunnuseks on see, et nad on kõik ühesugused, ainult erineva suurusega. Neid saab ümber paigutada ja muuta nende parameetrite täpsustamiseks, et need sobiksid mis tahes teise parabooliga. Paraboole kasutatakse mitmesugustes rakendustes, nagu auto esilaternate reflektorid, ballistiliste rakettide disain jne. Samuti mängivad nad olulist rolli füüsikas, inseneriteaduses, matemaatikas jne.

Hüperboolid on sile kõver, mis tekib siis, kui tasapind lõikub Y-teljega paralleelse koonusega, mis tekitab koonuse serva lõigatud. Hüperbool on määratletud selle geomeetriliste omaduste või võrranditega, mille jaoks see on lahendus. Mõiste "hüperbool" on tuletatud kreeka sõnast, mis tähendab "üleliigne" või "ülemäärane". Arvatakse, et selle mõiste on kujundanud Perga Apollonius, kes on suuresti kaasa aidanud koonusosade uurimisele.

On teada, et hüperboolal on filiaalid, mis on üksteisele peegelpildid ja sarnanevad kahe lõpmatu vibuga. Nende kahe haru punktid, mis on üksteisele kõige lähemal, nimetatakse tippudeks. Punkte ühendav joon on tuntud kui põiktelg või põhitelg, mis vastab ellipsi suuremale läbimõõdule. Risttelje keskpunkt on tuntud kui hüperbola keskus. Hüperbooli võrrand on kirjutatud kui x2 / a2- y2 / b2 = 1. Hüperboole kasutatakse tänapäeva maailmas mitmesugustes rakendustes, kaasa arvatud päikesekella tipu varju, avatud orbiidi kuju; seda kasutatakse kaarena paljudes ehitatud hoonetes, nagu matemaatika ja geomeetria, füüsika jne.

Hüperboolid ja paraboolid on mõlemad avatud kõverad, mis tähendab, et nad ei lõpe ja jätkavad lõpmatuseni, mida ellipsid ja ringid ei saa teha.