Peamine erinevus: punkt on punkt, mis tähistab lõpmatusse ruumi või tasapinnale märgitud asukohta. Liini peetakse ühemõõtmeliseks ja see tutvustati sirgete objektide esindamiseks, millel ei ole laiust ega sügavust. Tasapind on kahemõõtmeline tasane pind, mis on määramata ajaks nullpaksusega.

Punkt, joon ja lennuk on kõik terminid, mida tavaliselt matemaatikas leidub. Need moodustavad geomeetria põhiraami töö ja moodustavad suure osa eukleidise geomeetriast. Eukleidiline geomeetria on matemaatiline süsteem, mille auks on Aleksandria kreeka matemaatik Euklid. Ehkki paljud matemaatikud avastasid euklidesea tulemuste suure osa, oli ta esimene, kes võttis endale väikese hulga intuitiivselt ahvatlevaid aksioome ja tuletades nendest palju teisi ettepanekuid (teoreeme).

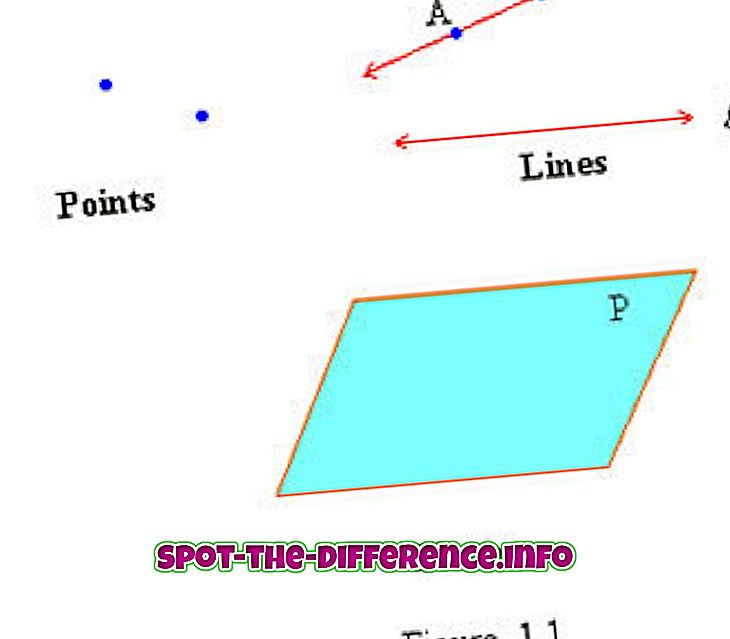
Punkti, joont ja tasapinda peetakse geomeetria määratlemata terminiks, sest neid ei ole ametlikult määratletud. Mõiste määratlemisel kasutatakse tavaliselt terminite kirjeldamiseks lihtsamaid sõnu. Punkti, joont ja lennukit loetakse siiski juba lihtsustatud terminiteks. Kõik teised geomeetrilised mõisted on ehitatud punktile, joonele ja tasandile. Proovime siiski mõista neid kolme määratlemata mõistet.

Punkt on punkt, mis ei tähenda asja, vaid positsiooni. Punkt tähistab asukohta, mis on märgitud lõpmatusse ruumi või tasapinnale. Punkt võib olla ükskõik millise suurusega punkt, kuid selle pikkus, laius või paksus puudub. See on sellepärast, et see esindab kohta ja mitte asja.

Punkte nimetatakse suurtähtedega A, B, C jne. Kahemõõtmelisel eukleidise ruumil, mida tuntakse paremini kui võrku või graafikut koos x-telje ja y-teljega, esindab punkti punkt tellitud paar (x, y). X tähistab punkti horisontaalset paigutust, samas kui y tähistab vertikaalset paigutust. Punkte on kahte rida: kollinaarne ja ühetasane. Kollektiivne punktide hulk paikneb sirgjoonel, samas kui ühetasapinnaline rida rida asub samal tasapinnal.

Liini peetakse ühemõõtmeliseks ja see tutvustati sirgete objektide esindamiseks, millel ei ole laiust ega sügavust. Liini määratlus sõltub geomeetria tüübist. Eukleidi geomeetria puhul ei ole liinil määratlust. Analüütilises geomeetrias määratletakse tasapinnal olev rida punktide kogumina, mille koordinaadid vastavad antud lineaarsele võrrandile. Sageduse geomeetria puhul võib rida olla iseseisev objekt, mis asub selle punktide hulgast.

Rida aktsepteeritakse ühemõõtmelise lõpmatu punktidena, mis on ühendatud. Sirge joon on kõige lühem vahemaa kahe punkti vahel lennukil. Liinid on iga lõpus märgitud kahe noolega, mis tähendab, et see ei lõpe kunagi. Liinid nimetatakse kahel viisil: kahe punkti võrra liinil või ühe väikese kirjaga. Joonele märgitud kahte punkti saab kasutada joonele viitamiseks. Näiteks: Rida punktidega H, I selle peal on märgistatud rida HI ja selle peale asetatakse see, mis tähendab, et see on rida.

Tasapind on kahemõõtmeline tasane pind, mis on määramata ajaks nullpaksusega. Tasandit peetakse punkti (nullmõõtmed), joone (ühemõõtmeline) ja tahke (kolmemõõtmeline) kahemõõtmeliseks analoogiks. Eukleidilise ruumi mõiste määratlemisel viitab lennuk kogu ruumile. Kujutage ette metallist leht, millel ei ole paksust, kuid see jätkub igavesti ja igavesti. Seda peetakse lennukiks.

Wikipedia väidab: „Paljud matemaatika, geomeetria, trigonomeetria, graafika teooria ja graafika põhiülesanded täidetakse kahemõõtmelises ruumis või teisisõnu tasapinnal.” Kuigi lennukid on joonistamise huvides lõpmatud, nõuavad nad servad. Need lennukid on joonistatud kahe paralleelse paariga ja näevad välja nagu kaldus ristkülik. Tasapinnal on kaks mõõdet: pikkus ja laius. Kuid kuna lennuk on lõputult suur, ei saa pikkust ja laiust mõõta.

Lennukeid määratletakse kolme punkti võrra. On kahte tüüpi lennukeid: paralleelsed tasapinnad ja ristuvad lennukid. Paralleelsed tasapinnad on kaks või enam lennukit, mis liiguvad lõputult ilma teineteise teed ületamata. Kujutage ette varasemat metalllehte, lisage nüüd veel üks metallplaat, mis on selle peal, ja jätkub ka igavesti. Need kaks teeksid kaks paralleelset tasapinda, mis kunagi ristuvad. Kuid huvitavad lennukid on täpselt nii. Need on kaks lennukit, mis ületavad teineteise teed. Lennukeid nimetatakse üldjuhul ühe suure kirjaga, mis on kirjutatud kursiivis (Plane P).

Geomeetrias liidetakse punkt, joon ja lennuk postulaadi kujul. See postulaat on kolme eelduse (aksioomide) kogum, mida saab kasutada osana eukleidise geomeetria kolmest või enamast mõõtmest. Kolm eeldust on järgmised: Unikaalne rea eeldus, arvuliini eeldus ja mõõtme eeldus. Unikaalne rea eeldus viitab sellele, et kaks erinevat punkti läbivad täpselt ühe rea. Numbrirea eeldus näitab, et iga rida on punktide kogum, mida saab panna reaalarvudega vastavusse. Iga punkt võib vastata 0-le (null) ja mis tahes muu punkt võib vastata 1-le (ühele). Lõpuks, mõõtu eeldused annavad tasapinnal rida, vähemalt tasapinnal, mis ei ole liinil, on olemas vähemalt üks punkt. Arvestades tasapinda kosmoses, on vähemalt üks punkt ruumis, mis ei ole lennukis.